Bisector of ∠ BAC of ΔABC and the straight line through the midpoint D of the side AC the parallel to the side AB meet at a point E, outside BC. Let’s prove that ∠ AEC = 1 right angle.

Question

Philoid · Accepted Answer

Given: ΔABC, the bisector of ∠BAC, D is the midpoint of side AC, line parallel to side AB through point D, the bisector and parallel line meet at point E outside BC

To prove ∠AEC = 1 right angle, i.e., ∠AEC = 90°

In ΔABC, let AE be the bisector of ∠BAC,

Let DE be the parallel line to side AB though point D, where D is the midpoint of AC.

So the figure of the given question is as shown below,

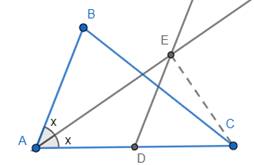
Given AE is the bisector of ∠BAC, so let

∠BAE = ∠EAC = x……….(i)

Given DE||AB and with AE as the transversal line,

Then ∠BAE = ∠AED = x ……..(ii) (as they form alternate interior angles)

Now consider ΔADE,

From equation (ii),

∠BAE = ∠AED = x

We know sides opposite to equal angles are equal, so

AD = DE………(iii)

And in same triangle ∠EDC form external angle, but we know the measure of any exterior angle of a triangle is equal to the sum of the measures of its two interior opposite angles, so

∠EDC = ∠EAD + ∠AED

Now substituting values from equation (i) and (ii), we get

∠EDC = x + x = 2x….(iv)

Now consider ΔAEC, given D is midpoint of AC,

So AD = DC……(iv)

We know angles opposite to equal sides are equal, so

∠AED = ∠DEC

Now substituting the value from equation (ii), we get

∠AED = DEC = x………(v)

By comparing equation (iii) and (iv), we get

DE = DC…..(v)

Now consider ΔDEC

We also know angles opposite to equal sides are equal, so from equation (v), we get

∠DEC = ∠ECD

Now substituting the value from equation (ii), we get

∠DEC = ∠ECD = x……….(vi)

Now in ΔEDC,

We know in a triangle the sum of all three interior angles is equal to 180°.

So in this case,

∠EDC + ∠DEC + ∠ECD = 180°

Substituting value from equation (iv) and (vi) in above equation we get

2x + x + x = 180°

⇒ 4x = 180°

⇒ x = 45°……….(vii)

Now from figure,

∠AEC = ∠AED + ∠DEC

Substituting values from equation (v), we get

∠AEC = x + x = 2x

Substituting values from equation (vii), we get

∠AEC = 2(45°) = 90°

Hence ∠AEC = 1 right angle

Hence proved

Bisector of ∠BAC of ΔABC and the straight line through the midpoint D of the side AC the parallel to the side AB meet at a point E, outside BC. Let’s prove that ∠AEC = 1 right angle.