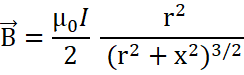Using Biot-Savart’s law, derive an expression for magnetic field at any point on axial line of a current carrying circular loop. Hence, find magnitude of magnetic field intensity at the centre of circular coil.

According to Biot-savart’s law, the current carrying wire generates magnetic field which is directly proportional to the strength of the current (i), length of the element (dl), angle between the element and the line joining the element and the point. And it is inversely proportional tot hr square of the distance between the point and the element.

In vector form,

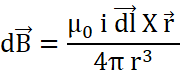
To find magnetic field at any point on axial line of a current carrying circular loop:

Consider a current (I) carrying circular coil of radius r. Let there is a point P, at a distance x from the centre of the coil. Consider the circular loop made up of small element dl, carrying current dI and these small elements generate small magnetic field dB. The sum of all these fields at the point will give the total magnetic field at that point. At the centre of the coil, the field will be uniform. As the location of the point increases from the centre of the coil, the field decreases.

By Biot- Savart’s law, the field dB due to a small element dl of the circle, centred at A is given by,

it can be resolved in two components, vertical and horizontal. The vertical components will be cancelled by the opposite element’s vertical components. Therefore,

the total magnetic field at a point which is at a distance x away from the axis of a circular coil of radius r is given by