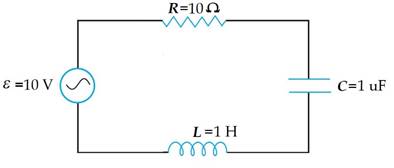
A sinusoidal voltage of peak value 10 V is applied to a series LCR circuit in which resistance, capacitance and inductance have values of 10 Ω, 1μF and 1H respectively. Find (i) the peak voltage across the inductor at resonance (ii) quality factor of the circuit.
Given:
Voltage, V=10 v
Resistance, R= 10 Ω
Inductive impedance=1 H
Capacitor =1 uF
Fomula used:
1. Angular velocity, w0=![]() … (1)
… (1)
Where,
L is the inductive impedance
C is capacitor impedance.
2. Peak current,![]() … (2)
… (2)
Where,
Vpeak is the peak current
R is the resistance
3. Voltage across inductor, Vinductor=Ipeak × w0L … (3)
Where,
Ipeak is the peak currents
w0 is the angular frequency
L is the inductive impedance
4.The quality factor of the circuit is given as,
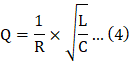
Where,
Q is the quality factor,
R is the resistance,
C is the capacitance, and L is the inductance.
Putting the value in equation 1, we get
![]()
The net current in circuit only depends upon the resistance as the circuit is in resonance,
Putting the value in equation 2
![]()
Now the rms voltage drop across the inductor is given as,
Putting the value in equation 3, we get
![]()
![]()
Also, the quality factor Q (which is ratio of reactance to resistance) of the given series LCR circuit given by equation 4 is as,
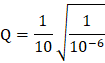
![]()
So, Q = 100.
Conclusion: -
The peak voltage across the inductor at resonance is 1000 V.
The quality factor of the circuit is, Q = 100.