Find the area of the greatest rectangle that can be inscribed in an ellipse

OR

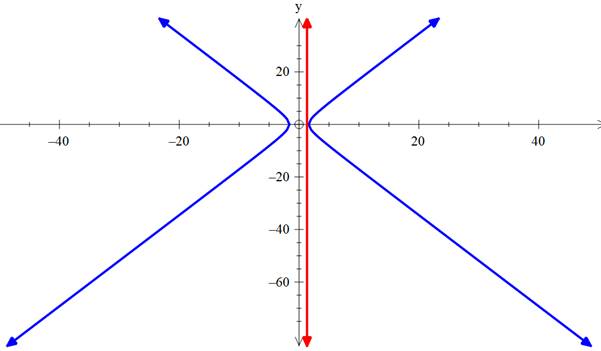
Find the equations of tangents to the curve 3x² – y² = 8, which pass through the point

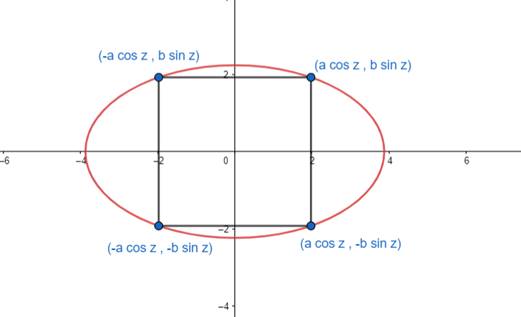
As we know that: For a given ellipse we can give the coordinates of a point on the given ellipse by (acos θ, bsin θ)

From figure we can say that length of rectangle = 2a cosθ

Note: In reference to figure - (taking z = θ)

And breadth of inscribed rectangle = 2b sinθ

Let A be the area of rectangle inscribed.

∴ A = 4ab sinθ cos θ = 2ab sin 2θ

We need to maximise the area.

∴

⇒

⇒ 4ab cos 2θ = 0

⇒ cos 2θ = 0

∴ θ = π/4

Clearly,

And

∴ θ = π/4 is the point of maxima.

Hence area of the greatest rectangle that can be inscribed in the given ellipse is given by

A = 2ab sin(2×π/4) = 2ab.

OR

Given equation is 3x² – y² = 8.

To find the equation of tangent we need to find the slope first and the slope is given by the value of derivative at that point.

As, 3x² – y² = 8

Differentiating both sides w.r.t x, we get –

⇒

⇒

∴

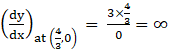
As slope comes to be infinite ⇒ line is parallel to y – axis

Given that it passes through (4/3,0)

∴ line parallel to y-axis and passing through (4/3,0) is

x = 4/3