Using the properties of determinants in evaluate:
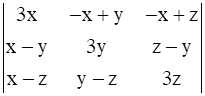
Let
By applying C1→ C1 + C2 + C3, we have


Taking (x + y + z) common from Column C1, we get

By applying R2→ R2 – R1, we get



By applying R3→ R3 – R1, we get



Applying C2→ C2 – C3, we get



Now, expanding along C1, we get
= (x + y + z) [1×{(3y)(2z + x) – (-3z)(x – y)}]
= (x + y + z) [6yz + 3yx + (3z)(x – y)]
= (x + y + z) [6yz + 3yx + 3zx – 3zy]
= (x + y + z) [3yz + 3zx + 3yx]
= 3(x + y + z)(yz + zx + yx)
4