Using the properties of determinants in evaluate:

Question

Philoid · Accepted Answer

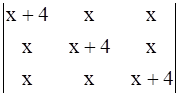
By applying C₁→ C₁ + C₂ + C₃, we get

Taking (3x + 4) common from first column, we get

By applying R₂→ R₂ – R₁, we get

By applying R₃→ R₃ – R₁, we get

Now, expanding along first column, we get

= (3x + 4) [1×{(16) – 0}]

= (3x + 4)(16)

= 16(3x + 4)