If x + y + z = 0, prove that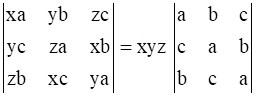

Given: x + y + z = 0

To Prove:

Taking LHS,

Expanding along the first row, we get

= xa{(za)(ya) – (xc)(xb)} – (yb){(yc)(ya) – (zb)(xb)} + (zc){(yc)(xc) – (zb)(za)}

= xa{a²yz – x²bc} – yb{y²ac – b²xz} + zc{c²xy – z²ab}

= a³xyz – x³abc – y³abc + b³xyz + c³xyz – z³abc

= xyz(a³ + b³ + c³) – abc(x³ + y³ + z³)

It is given that x + y + z = 0

⇒ x³ + y³ + z³ = 3xyz

= xyz(a³ + b³ + c³) – abc (3xyz)

= xyz(a³ + b³ + c³ – 3abc)

Hence Proved