The value of determinant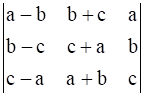

We have,

Applying C₂→ C₂ + C₃, we get

Taking (a + b + c) common from second column, we get

Applying C₁ → C₁ – C₃, we get

Expanding along first row, we get

= (a + b + c)[(-b){c – b} – (1){-c² – (-ab)} + a{-c – (-a)}]

= (a + b + c)(-bc + b² + c² – ab – ac + a²)

= a(-bc + b² + c² – ab – ac + a²) + b(-bc + b² + c² – ab – ac + a²) + c(-bc + b² + c² – ab – ac + a²)

= -abc + ab² + ac² – a²b – a²c + a³ – b²c + b³ + bc² – ab² – abc + a²b – bc² + b²c + c³ – abc – ac² + a²c

= a³ + b³ + c³ – 3abc

Hence, the correct option is (c)