The number of distinct real roots of 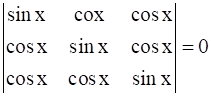 in the interval
in the interval 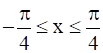 is
is
We have, 
Applying C1→ C1 + C2 + C3, we get


Taking (2cos X + sin X) common from the first column, we get

Applying R2→ R2 – R1, we get


Applying R3→ R3 – R1, we get


Expanding |A| along C1, we get
⇒ (2cos X + sin X) [(1){(sin X – cos X)(sin X – cos X)}]
⇒ (2cos X + sin X)(sin X – cos X)2 = 0
⇒ 2cos X = -sin X or (sin X – cos X)2 = 0
![]()
⇒ tan X = -2 or tan X = 1 ![]()
but tan X = -2 is not possible as for ![]()
So, tan X = 1
![]()
Hence, only one real distinct root exist.
Hence, the correct option is (c)
28