Show that f (x) = tan^–1(sin X + cos X) is an increasing function in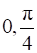

Given: f (x) = tan^–1(sin X + cos X)

To show: the given function is increasing in .

Explanation: Given f (x) = tan^–1(sin X + cos X)

Applying first derivative with respect to x, we get

Applying the differentiation rule for tan^-1, we get

Applying the sum rule of differentiation, we get

But the derivative of sin X = cos x and that of cos x = -sin x, so

Expanding (sin x+cos x )², we get

But sin²x+cos²x = 1 and 2sin Xcos X = sin2x, so the above equation becomes,

Now for f(x) to be decreasing function,

f’(x)≥0

⇒ cos x- sin x≥ 0

⇒ cos x≥ sin x

But this is possible only if

Hence the given function is increasing function in .