At 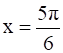, f (x) = 2 sin3x + 3 cos3x is:

Given f (x) = 2 sin3x + 3 cos3x

Applying the first derivative we get

Applying the sum rule of differentiation and taking out the constant terms, we get

Applying the derivative,

⇒ f' (x)=2.cos3x.3-3.sin3x.3

⇒ f’(x)=6cos3x-9sin3x……(i)

Now we will find the value of f’(x) at , we get

Now split

Now we know cos(2π+θ)=cosθ and sin(2π+θ)=sinθ

Now we know and

And we find that f’(x) at is not equal to 0.

So cannot be point of maxima or minima.

Hence, f (x) = 2 sin3x + 3 cos3x at is neither maxima nor minima.

So the correct option is option D.