Prove that in any triangle ABC,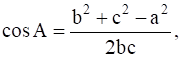 
where a, b, c are the magnitudes of the sides opposite to the vertices A, B, C, respectively
Given:
a, b, c are magnitudes of the sides opposite to the vertices A, B, C respectively.
⇒ AB = c, BC = a and CA = b
To Prove:
In triangle ABC,
Construction: We have constructed a triangle ABC and named the vertices according to the question.
Note the height of the triangle, BD.
If ∠BAD = A
Then, BD = c sin A
[∵ 
in ∆BAD
⇒ BD = c sin A]
And, AD = c cos A
[∵ 
in ∆BAD
⇒ AD = c cos A]
Proof:
Here, components of c which are:
c sin A
c cos A
are drawn on the diagram.
Using Pythagoras theorem which says that,
(hypotenuse)2 =(perpendicular)2 + (base)2
Take ∆BDC, which is a right-angled triangle.
Here,
Hypotenuse = BC
Base = CD
Perpendicular = BD
We get,
(BC)2 = (BD)2 + (CD)2
⇒ a2 = (c sin A)2 + (CD)2 [∵ from the diagram, BD = c sin A]
⇒ a2 = c2 sin2 A + (b – c cos A)2
[∵ from the diagram, AC = CD + AD
⇒ CD = AC – AD
⇒ CD = b – c cos A]
⇒ a2 = c2 sin2 A + (b2 + (-c cos A)2 – 2bc cos A) [∵ from algebraic identity, (a – b)2 = a2 + b2 – 2ab]
⇒ a2 = c2 sin2 A + b2 + c2 cos2 A – 2bc cos A
⇒ a2 = c2 sin2 A + c2 cos2 A + b2 – 2bc cos A
⇒ a2 = c2 (sin2 A + cos2 A) + b2 – 2bc cos A
⇒ a2 = c2 + b2 – 2bc cos A [∵ from trigonometric identity, sin2 θ + cos2 θ = 1]
⇒ 2bc cos A = c2 + b2 – a2
⇒ 2bc cos A = b2 + c2 – a2
Hence, proved.