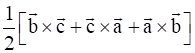If determine the vertices of a triangle, show that gives the vector area of the triangle. Hence deduce the condition that the three points a, b, c are collinear. Also find the unit vector normal to the plane of the triangle.

Question

Philoid · Accepted Answer

Let are vertices of a triangle ABC.

Also, we get

Position vector of A

Position vector of B

Position vector of C

We need to show that,

gives the vector are of the triangle.

We know that,

Vector area of ∆ABC is given as,

Here,

…(i)

Thus, shown.

We know that, two vectors are collinear if they lie on the same line or parallel lines.

For to be collinear, area of the ∆ABC should be equal to 0.

⇒ Area of ∆ABC = 0

…(ii)

Thus, this is the required condition for to be collinear.

Now, we need to find the unit vector normal to the plane of the triangle.

Let be the unit vector normal to the plane of the triangle.

Note that, from equation (i).

And, from equation (i).

So,

Thus, unit vector normal to the plane of the triangle is .