The mean and standard deviation of some data for the time taken to complete a test are calculated with the following results:
Number of observations = 25, mean = 18.2 seconds, standard deviation = 3.25 seconds.
Further, another set of 15 observations x1, x2, ..., x15, also in seconds, is now available and we have
and 
. Calculate the standard derivation based on all 40 observations.
Given: Number of observations = 25, mean = 18.2 seconds, standard deviation = 3.25 seconds. Another set of 15 observations x1, x2, ..., x15, also in seconds, is 
and 
To find: the standard derivation based on all 40 observations
As per the given criteria,
In first set,
Number of observations, n1=25
Mean,
And standard deviation,
And
In second set,
Number of observations, n2=15
and 
For the first set we have
∑xi=25×18.2=455
Therefore the standard deviation becomes,
Substituting the values, we get
For the combined standard deviation of the 40 observation, n=40
And
Therefore the standard deviation can be written as,
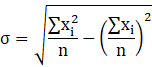
Substituting the values, we get
Therefore the standard deviation can be written as,
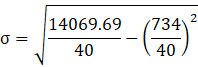
σ=3.87
Hence the standard derivation based on all 40 observations is 3.87.