Find the locus of point ℓ equidistant from three vertices and three sides of a triangle.

The locus of point ℓ equidistant from three vertices is the circumcentre and three sides of a triangle is the incentre of the triangle.

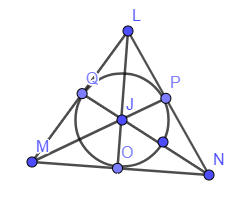
Here, J is the incentre of the ∆LMN.

At first draw the angle bisectors of all the angles i.e, ∠L , ∠M and ∠N.

LO, MP and NQ are the angle bisectors respectively.

Let LO, MP and NQ intersect at J,

∴ J is the incentre.

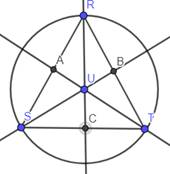
Here, U is the circumcenter of the ∆RST.

At first , draw the perpendicular bisectors of the sides ST, RT and RS of the triangle.

Here, RC, SB and AT are the required perpendicular bisectors.

Lat them intersect at U

Hence, U is the circumcenter of the triangle.