In figure 3.95, chord EF || chord GH. Prove that, chord EG ≅ chord FH.
Fill in the blanks and write the proof.
Proof : Draw seg GF.
∠ EFG = ∠ FGH ...Alternate interior angles.......![]() (I)
(I)
∠ EFG = …………90° ………{inscribed angle theorem}(II)
∠ FGH = …………… 90° ………….{inscribed angle theorem} (III)
∴m(arc EG) = ……………90°…………. from (I), (II), (III).
chord EG ≅ chord FH ..........![]()
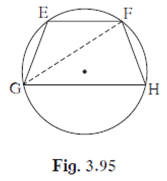
Proof : Draw seg GF.
∠ EFG = ∠ FGH {Alternate interior angles} (I)
∠ EFG = 90°{inscribed angle theorem}(II)
∠ FGH = 90°{inscribed angle theorem} (III)
∴m(arc EG) = 90° from (I), (II), (III).
chord EG ≅ chord FH {Corresponding chords of congruent arcs of a circle (or congruent circles) are congruent}
1