In figure 3.100, two circles intersect each other at points S and R. Their common tangent PQ touches the circle at points P, Q.
Prove that, ∠ PRQ + ∠ PSQ = 180°

Question

In figure 3.100, two circles intersect each other at points S and R. Their common tangent PQ touches the circle at points P, Q. Prove that, ∠ PRQ + ∠ PSQ = 180°

Philoid · Accepted Answer

We join R to S,

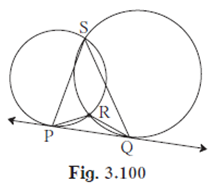
As PQ is the tangent at P, we have

∠RPQ = ∠PSR …………..(1)

As PQ is tangent at Q, we have

∠RQP = ∠RSQ …………………(2)

In ΔRPQ, we have

⇒ ∠RPQ + ∠RQP + ∠ PRQ = 180° (Sum of all angles of a triangle)

⇒ ∠PSR + ∠RSQ + ∠PRQ = 180° (From (1) and (2))

⇒ ∠PSQ + ∠PRQ = 180° (∠PSR + ∠RSQ = ∠PSQ)

Hence Proved.

In figure 3.100, two circles intersect each other at points S and R. Their common tangent PQ touches the circle at points P, Q.Prove that, ∠ PRQ + ∠ PSQ = 180°

In figure 3.100, two circles intersect each other at points S and R. Their common tangent PQ touches the circle at points P, Q.
Prove that, ∠ PRQ + ∠ PSQ = 180°