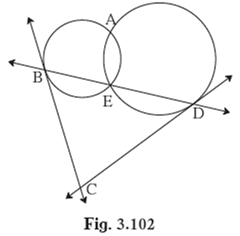
In figure 3.102, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points Band D intersect each other at point C.
Prove that ABCD is cyclic.

Question

Philoid · Accepted Answer

We join A to B and A to D and A to E

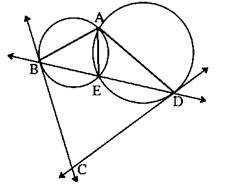
As BC is a tangent at B, we have

∠ CBD = ∠BAE ………….(1)

As CD is a tangent at D, we have

∠ CDB = ∠DAE ………….(2)

In ΔBCD, we have

⇒ ∠CBD + ∠CDB + ∠ BCD = 180° (Sum of all angles of a triangle)

⇒ ∠BAE + ∠DAE + ∠BCD = 180° (From (1) and (2))

⇒ ∠BAD + ∠BCD = 180° (∠BAE + ∠DAE = ∠BAD)

In quadrilateral ABCD,

We have ∠A + ∠C = 180° (Proved above)

⇒ ∠A + ∠B + ∠C + ∠D = 360°

⇒ ∠B + ∠D + 180 = 360

⇒ ∠B + ∠D = 180

Therefore, opposite angles of the quadrilateral sum to 180. Hence ABCD is a cyclic quadrilateral.

In figure 3.102, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points Band D intersect each other at point C.Prove that ABCD is cyclic.