A side of an equilateral triangle is 20cm long. A second equilateral triangle is inscribed in it by joining the mid points of the sides of the first triangle. The process is continued as shown in the accompanying diagram. Find the perimeter of the sixth inscribed equilateral triangle.

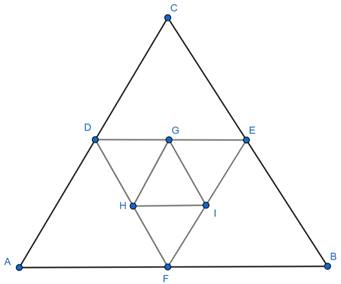
Let ABC be the triangle with AB = BC = AC = 20 cm

Let D, E and F be midpoints of AC, CB and AB respectively which are joined to form an equilateral triangle DEF

We have to find the length of side of ΔDEF

Consider ΔCDE

CD = CE = 10 cm … D and E are midpoints of AC and CB

Hence ΔCDE is isosceles

⇒ ∠CDE = ∠CED … base angles of isosceles triangle

But ∠DCE = 60° …∠ABC is equilateral

Hence ∠CDE = ∠CED = 60°

Hence ΔCDE is equilateral

Hence DE = 10 cm

Similarly, we can show that GH = 5 cm

Hence the series of sides of equilateral triangle will be

20, 10, 5, …

The series is GP with first term a = 20 and common ratio r = 1/2

To find the perimeter of 6^th triangle inscribed we first have to find the side of 6^th triangle that is the 6^th term in the series

n^th term in GP is given by t_n = ar^n-1

⇒ t₆ = (20)(1/2)^6-1

Hence the side of 6^th equilateral triangle is cm and hence its perimeter would be thrice its side length because its an equilateral triangle

Perimeter of 6^th equilateral triangle inscribed is