If , where c is real, prove that a 2 + b 2 = 1 and .

Question

Philoid · Accepted Answer

Consider the given equation,

Now, rationalizing

[(a – b)(a + b) = a² – b²]

[i² = -1]

On comparing both the sides, we get

Now, we have to prove that a² + b² = 1

Taking LHS,

a² + b²

Putting the value of a and b, we get

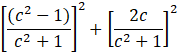
= 1

= RHS

Now, we have to prove

Taking LHS,

Putting the value of a and b, we get

Hence Proved

If , where c is real, prove that a2 + b2 = 1 and .