Find the smallest positive integer n for which (1 + i)2n = (1 – i)2n.
Given: (1 + i)2n = (1 – i)2n
Consider the given equation,
(1 + i)2n = (1 – i)2n
![]()
![]()
Now, rationalizing by multiply and divide by the conjugate of (1 – i)
![]()
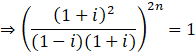
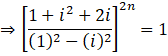
[(a + b)2 = a2 + b2 + 2ab & (a – b)(a + b) = (a2 – b2)]
![]() [i2 = -1]
[i2 = -1]
![]()
⇒ (i)2n = 1
Now, i2n = 1 is possible if n = 2 because (i)2(2) = i4 = (-1)4 = 1
So, the smallest positive integer n = 2
1