Find the domain and range of each of the relations given below:
(i) R = {(–1, 1), (1, 1), (–2, 4), (2, 4), (2, 4), (3, 9)}

(ii)

(iii) R ={(x, y) : x + 2y = 8 and x, y ϵ N}

(iv) R = {(x, y), : y = |x – 1|, x ϵ Z and |x| ≤ 3}

Question

Philoid · Accepted Answer

(i) Given: R = {(–1, 1), (1, 1), (–2, 4), (2, 4), (2, 4), (3, 9)}

Dom(R) = {x: (x, y) R} = {-2, -1, 1, 2, 3}

Range(R) = {y: (x, y) R} = {1, 4, 9}

(ii) Given: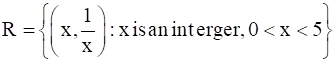

That means,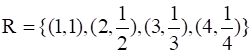

Dom(R) = {x: (x, y) R} = {1, 2, 3, 4}

Range(R) = {y: (x, y) R} = {1, , , }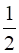

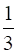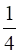(iii) Given: R = {(x, y): x + 2y = 8 and x, y ϵ N}

That means, R = {(2, 3), (4, 2), (6, 1)}

Dom(R) = {x: (x, y) R} = {2, 4, 6}

Range(R) = {y: (x, y) R} = {1, 2, 3}

(iv) Given: R = {(x, y): y = |x – 1|, x ϵ Z and |x| ≤ 3}

Dom(R) = {x: (x, y) R} = {-3, -2, -1, 0, 1, 2, 3}

Range(R) = {y: (x, y) R} = {0, 1, 2, 3, 4}

Find the domain and range of each of the relations given below:(i) R = {(–1, 1), (1, 1), (–2, 4), (2, 4), (2, 4), (3, 9)}(ii) (iii) R ={(x, y) : x + 2y = 8 and x, y ϵ N}(iv) R = {(x, y), : y = |x – 1|, x ϵ Z and |x| ≤ 3}