Find the modulus of each of the following complex numbers and hence express each of them in polar form:

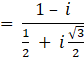
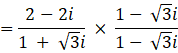
Let

Now , separating real and complex part , we get

……….eq.1

…………eq.2

Squaring and adding eq.1 and eq.2, we get

2 = r²

Since r is always a positive no., therefore,

r = √2,

hence its modulus is √2.

now, dividing eq.2 by eq.1 , we get,

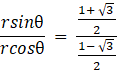
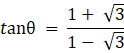
Since , and tanθ =. therefore the θ lies in second quadrant. As

, therefore

Representing the complex no. in its polar form will be

}