In how many ways can the letters of the word ‘INTERMEDIATE’ be arranged so that:
(i) the vowels always occupy even places?
(ii) the relative orders of vowels and consonants do not change?
(i)
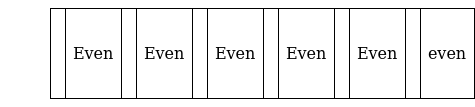
There are 6 even places and 6 vowels out of which 2 are of 1 kind, 3 are of the 2nd kind
The vowels can be arranged in 
60
There are 6 consonants out of which 2 is of one kind
Number of permutations = 
360
Total number of words = 
(ii)
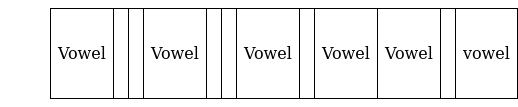
There are 6 vowels to arrange in 
There are 6 consonants which can be arranged in 
Total number of ways = 
21600
1