Write first 4 terms in each of the sequences:

(i) a_{n =} (5n + 2)

(ii) a_n =

(iii) a_n = (–1)^n–1 × 2^{n + 1}

To Find: First four terms of given series.

(i) Given: n^th term of series is (5n + 2)

Put n=1, 2, 3, 4 in n^th term, we get first (a1), Second (a2), Third (a3) & Fourth (a4) term

a₁ = (51 + 2) = 7

a₂ = (52 + 2) = 12

a₃ = (53 + 2) = 17

a₄ = (54 + 2) = 22

First four terms of given series is 7, 12,17,22

ALTER: When you find or you have first term (a or a₁) and second term (a₂) then find the difference (a₂ - a₁)

Now add this difference in last term to get the next term

For example a₁= 7 and a₂= 12, so difference is 12 - 5 = 7

Now a₃ = 12 + 5 = 17, a₄ = 17 + 5 = 22

(This method is only for A.P)

NOTE: When you have nth term in the form of (an + b)

Then common difference of this series is equal to a.

This type of series is called A.P (Arithmetic Progression)

(Where a, b are constant, and n is number of terms)

(ii) Given: n^th term of series is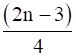

Put n=1, 2, 3, 4 in n^th term, we get first (a1), Second (a2), Third (a3) & Fourth (a4) term.

a₁ = =

a₂ = =

a₃ = =

a₄ = =

First four terms of given series are , , ,

(iii) Given: n^th term of series is (–1)^n–1 × 2^{n + 1}

Put n=1, 2, 3, 4 in n^th term, we get first (a1), Second (a2), Third (a3) & Fourth (a4) term.

a₁ = (–1)^1–1 × 2^{1 + 1} = (–1)⁰ × 2² = 14 = 4

a₂ = (–1)^2–1 × 2^{2 + 1} = (–1)¹ × 2³ = (–1)8 = (–8)

a₃ = (–1)^3–1 × 2^{3 + 1} = (–1)² × 2⁴ = 116 = 16

a₄ = (–1)^4–1 × 2^{4 + 1} = (–1)³ × 2⁵ = (–1)32 = (–32)

First four terms of given series are 4, –8 , 16 ,–32