The 4th and 7th terms of a GP are  and
and  respectively. Find the sum of n terms of the GP.
respectively. Find the sum of n terms of the GP.
4th term = ar4-1 = ar3 = ![]()
7th term = ar7-1= ar6 = ![]()
Dividing the 7th term by the 4th term,

⇒![]() ……(i)
……(i)
∴ ![]()
ar3 = ![]() [putting from eqn (i) ]
[putting from eqn (i) ]
a ![]() =
= ![]()
∴ a = 1
Sum of a G.P. series is represented by the formula, ![]() , when |r|<1. ‘Sn’ represents the sum of the G.P. series upto nth terms, ‘a’ represents the first term, ‘r’ represents the common ratio and ‘n’ represents the number of terms.
, when |r|<1. ‘Sn’ represents the sum of the G.P. series upto nth terms, ‘a’ represents the first term, ‘r’ represents the common ratio and ‘n’ represents the number of terms.
Here,
a = 1
![]()
n terms
∴ 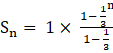
⇒
⇒![]()
∴ ![]()
1