If a, b, c are in GP, prove that
(i) a(b2 + c2) = c(a2 + b2)
(ii) 
(iii) (a + 2b + 2c)(a – 2b + 2c) = a2 + 4c2
(i) a(b2 + c2) = c(a2 + b2)
To prove: a(b2 + c2) = c(a2 + b2)
Given: a, b, c are in GP
Formula used: When a,b,c are in GP, b2 = ac
When a,b,c are in GP, b2 = ac
Taking LHS = a(b2 + c2)
= a(ac + c2) [b2 = ac]
= (a2c + ac2)
= c(a2 + ac)
= c(a2 + b2) [b2 = ac]
= RHS
Hence Proved
(ii) ![]()
To prove: a(b2 + c2) = c(a2 + b2)
Given: a, b, c are in GP
Formula used: When a,b,c are in GP, b2 = ac
Proof: When a,b,c are in GP, b2 = ac
Taking LHS = ![]()
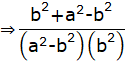
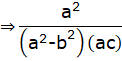
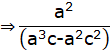
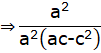
![]() [b2 = ac]
[b2 = ac]
Hence Proved
(iii) (a + 2b + 2c)(a – 2b + 2c) = a2 + 4c2
To prove: (a + 2b + 2c)(a – 2b + 2c) = a2 + 4c2
Given: a, b, c are in GP
Formula used: When a,b,c are in GP, b2 = ac
Proof:When a,b,c are in GP, b2 = ac
Taking LHS = (a + 2b + 2c)(a – 2b + 2c)
⇒ [(a + 2c) + 2b] [(a + 2c) – 2b]
⇒ [(a + 2c)2 – (2b)2] [(a + b) (a – b) = a2 – b2]
⇒ [(a2 + 4ac + 4c2) – 4b2]
⇒ [(a2 + 4ac + 4c2) – 4b2] [ b2 = ac]
⇒ [(a2 + 4ac + 4c2 – 4ac]
⇒ a2 + 4c2 = RHS
Hence Proved
(iv)![]()
To prove: ![]()
Given: a, b, c are in GP
Formula used: When a,b,c are in GP, b2 = ac
Proof: When a,b,c are in GP, b2 = ac
Taking LHS = ![]()
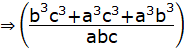
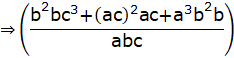
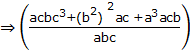 [b2 = ac]
[b2 = ac]
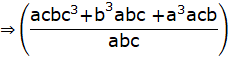
![]() = RHS
= RHS
Hence Proved
