The AM between two positive numbers a and b(a>b) is twice their GM. Prove that a:b ![]() .
.
To prove: Prove that a:b ![]()
Given: Arithmetic mean is twice of Geometric mean.
Formula used: (i) Arithmetic mean between ![]()
(ii) Geometric mean between ![]()
AM = 2(GM)
![]()
⇒ a + b = 4![]()
Squaring both side
⇒ (a + b)2 = 16ab … (i)
We know that (a – b)2 = (a + b)2 – 4ab
From eqn. (i)
⇒ (a – b)2 = 16ab – 4ab
⇒ (a – b)2 = 12ab … (ii)
Dividing eqn. (i) and (ii)
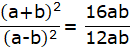
⇒ ![]()
Taking square root both side
![]()
![]()
Applying componendo and dividend
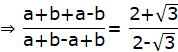
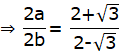
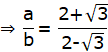
Hence Proved
1