Find the rational number whose decimal expansion is given below :
(i) ![]() (ii)
(ii) ![]()
(iii) ![]()
(i) Let, x=0.3333…
⇒ x=0.3+0.03+0.003+…
⇒ x=3(0.1+0.01+0.001+0.0001+…∞)
⇒ x=3(![]() )
)
This is an infinite geometric series.
Here, a=1/10 and r=1/10

∴x![]()
![]() =
=![]()
(ii) Let, x=0.231231231….
⇒ x=0.231+0.000231+0.000000231+…∞
⇒ x=231(0.001+0.000001+0.000000001+…∞)
⇒ x=231(![]() +
+![]() +…∞)
+…∞)
This is an infinite geometric series.
Here, a![]() and r=
and r=![]()
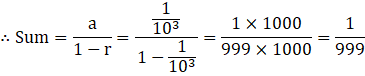
⇒ ![]()
![]() =
=![]()
(iii) Let, x=3.525252552…
⇒ x=3+0.52+0.0052+0.000052+…∞
⇒ x=3+52(0.01+0.0001+…∞)
⇒ x=3+52(![]() +
+![]() +…∞)
+…∞)
Here, a![]() and r=
and r=![]()

⇒ ![]()
![]()
![]()
1