Find the sum of the series whose nth term is given by:

(n³ – 3ⁿ)

It is given in the question that the n^th term of the series,

a_n = n³ – 3ⁿ

Now, we need to find the sum of this series, S_n.

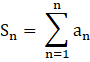
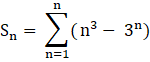
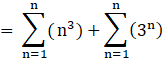
Note:

I. Sum of first n natural numbers, 1 + 2 +3+…n,

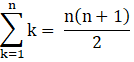
II. Sum of squares of first n natural numbers, 1² + 2² + 3²+….n²,

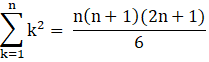
III. Sum of cubes of first n natural numbers, 1³ + 2³ + 3³ +…..n³,

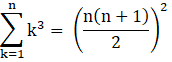
IV. Sum of a constant k, N times,

So, for the given series, we need to find,

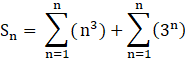
→ (1)

The second term in the equation,,

forms a GP, with the common ratio, r = 3.

Sum of n terms of a GP, a, ar, ar², ar³…arⁿ.

Here, a= 3, r = 3;

So,

→ (2)

Substitute (2) in (1);

Hence, the sum of the series,