Show that A(3, 2), B(0, 5), C(-3, 2) and D(0, -1) are the vertices of a square.

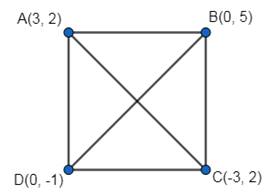
Given: The points are A(3, 2), B(0, 5), C(-3, 2) and D(0, -1).

Note: For a quadrilateral to be a square, all the sides of the quadrilateral must be equal in length and the diagonals must be equal in length as well.

AB

= 3√2 units

BC

= 3√2 units

CD

= 3√2 units

DA

= 3√2 units

Therefore, AB = BC = CD = DA …..(1)

AC

= 6 units

BD

= 6 units

Therefore, AC = BD …..(2)

From 1 and 2, we have all the sides of ABCD are equal and the diagonals are equal in length as well.

Therefore, ABCD is a square.

Hence, the points A, B, C and D are the vertices of a square.