Find the equation of the line whose portion intercepted between the axes is bisected at the point (3, -2).

Question

Philoid · Accepted Answer

To Find: The equation of the line whose portion intercepted between the axes is bisected at the point (3, -2).

Formula used:

Let the equation of the line be

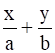= 1

Since it is given that this equation , whose portion is intercepted between the axes is bisected i.e.; is divided into ratio 1:1 .

Let A(a,0) and B(0,b) be the points foring the coordinate axis.

a and b are intercepts of x and y-axis respectively.

By using mid-point formula (m:n = 1:1)

(x, y) =( =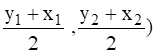

Since given point (3 , -2) divides coordinate axis in 1:1 ratio

(x , y) = (3 , -2)

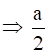=3 and = -2

a=6 b=-4

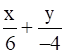equation of the line : = 1

= 1

-4x +6y = -24

-2x +3y = -12

Hence the required equation of the line is 2x -3y = 12.