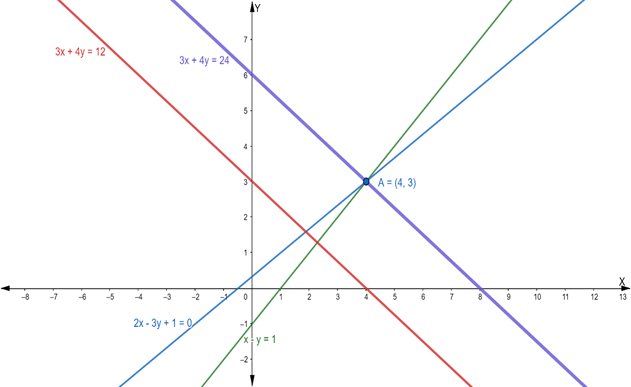
Find the equation of the line drawn through the point of intersection of the lines x – y = 1 and 2x – 3y + 1 = 0 and which is parallel to the line 3x + 4y = 12.
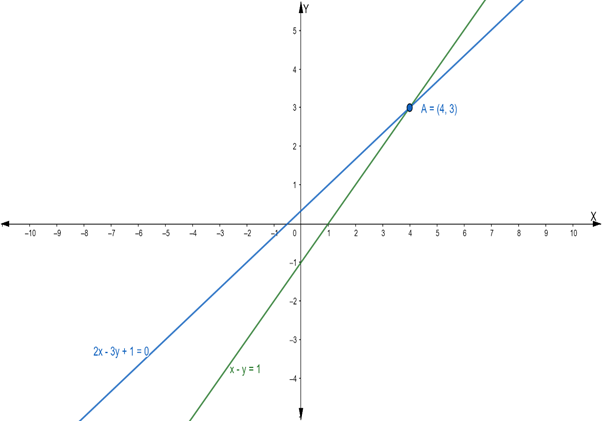
Suppose the given two lines intersect at a point P(x1, y1). Then, (x1, y1) satisfies each of the given equations.
x – y = 1 …(i)
2x – 3y + 1 = 0 …(ii)
Now, we find the point of intersection of eq. (i) and (ii)
Multiply the eq. (i) by 2, we get
2x – 2y = 2
or 2x – 2y – 2 = 0 …(iii)
On subtracting eq. (iii) from (ii), we get
2x – 3y + 1 – 2x + 2y + 2 = 0
⇒ -y + 3 = 0
⇒ y = 3
Putting the value of y in eq. (i), we get
x – 3 = 1
⇒ x = 1 + 3
⇒ x = 4
Hence, the point of intersection P(x1, y1) is (4, 3)
Now, we find the slope of the given equation 3x + 4y = 12
We know that the slope of an equation is
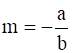
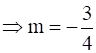
So, the slope of a line which is parallel to this line is also 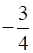
Then the equation of the line passing through the point (4, 3) having a slope 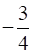 is:
is:
y – y1 = m (x – x1)
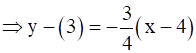
⇒ y – 3 = - 3x + 12
⇒ 4y – 12 = -3x + 12
⇒3x + 4y – 12 – 12=0
⇒ 3x + 4y – 24 = 0