Find the general solution of each of the following equations:

(i) sin 3x = 0

(ii)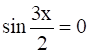

(iii)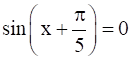

(iv) cos 2x = 0

(v)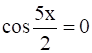

(vi)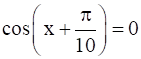

(vii) tan 2x = 0

(viii)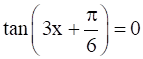

(ix)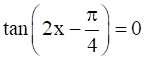

To Find: General solution.

[NOTE: A solution of a trigonometry equation generalized by means of periodicity, is known as general solution]

(i) Given: sin 3x = 0

Formula used: sin= 0 = n , n I

By using above formula, we have

sin 3x = 0 3x = n x = where n I

So general solution is x= where n I

(ii) Given: sin = 0

Formula used: sin= 0 = n , n I

By using above formula, we have

sin = 0 = n x = where n I

So general solution is x= where n I

(iii) Given: sin = 0

Formula used: sin= 0 = n , n I

By using the above formula, we have

sin = 0 = n x = n- where n I

So general solution is x= n- where n I

(iv) Given: cos 2x = 0

Formula used: cos= 0 = (2n+1) , n I

By using above formula, we have

cos 2x = 0 2x = (2n+1) x = (2n+1) where n I

So general solution is x= (2n+1)where n I

(v) Given: cos = 0

Formula used: cos= 0 = (2n+1) , n I

By using the above formula, we have

cos = 0 = (2n+1) x = (2n+1) where n I

So general solution is x= (2n+1)where n I

(vi) Given: cos = 0

Formula used: cos= 0 = (2n+1) , n I

By using the above formula, we have

cos = 0 = (2n+1) x = (2n+1) - x = n + where n I

So general solution is x= n + 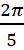where n I

(vii) Given: tan 2x = 0

Formula used: tan= 0 = n , n I

By using above formula, we have

tan 2x = 0 2x = n x = where n I

So general solution is x= where n I

(viii) Given: tan = 0

Formula used: tan= 0 = n , n I

By using above formula, we have

tan = 0 = n 3x = n - x = - where n I

So general solution is x = - where n I

(ix) Given: tan = 0

Formula used: tan= 0 = n , n I

By using above formula, we have

tan = 0 = n 2x = n - x = + where n I

So general solution is x = + where n I