Mark the tick against the correct answer in the following:

Let Q⁺ be the set of all positive rationals. Then, the operation * on Q⁺ defined by 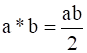for all a, b ∈ Q⁺ is

According to the question ,

Q = { Positive rationals }

R = {(a, b) : a * b = ab/2 }

Formula

* is commutative if a * b = b * a

* is associative if (a * b) * c = a * (b * c)

Check for commutative

Consider , a * b = ab/2

And , b * a = ba/2

Both equations are the same and will always true .

Therefore , * is commutative ……. (1)

Check for associative

Consider , (a * b) * c = (ab/2) * c = = abc/4

And , a * (b * c) = a * (bc/2) = = abc/4

Both the equation are the same and therefore will always be true.

Therefore , * is associative ……. (2)

Now , according to the equations (1) , (2)

Correct option will be (D)