If find the value of a and b such that A² + aA + bI = O.

Given : 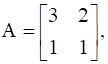A² + aA + bI = O

A is a matrix of order 2 x 2

To find : a and b

Formula used :

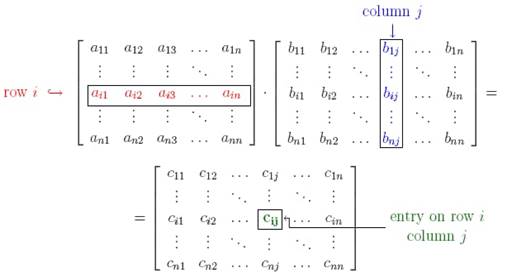
Where c_ij = a_i1b_1j + a_i2b_2j + a_i3b_3j + ……………… + a_inb_nj

If A is a matrix of order a b and B is a matrix of order c d ,then matrix AB exists and is of order a d ,if and only if b = c

A² is a matrix of order 2 x 2

A² = = =

A² =

aA = a =

bI = b =

bI =

A² + aA + bI = + + =

A² + aA + bI =

It is given that A² + aA + bI = 0

=

Equating similar terms in the matrices,we get

4 + a = 0 and 3 + a + b = 0

a = 0 – 4 = -4

a = -4

substituting a = -4 in 3 + a + b = 0

3 – 4 + b = 0

-1 + b = 0

b = 0 + 1 = 1

b = 1

a = -4 and b = 1