Using properties of determinants prove that:
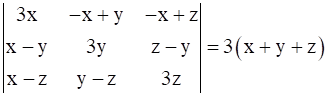
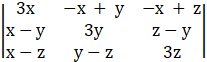
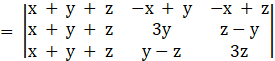[C1’ = C1 + C2 + C3]
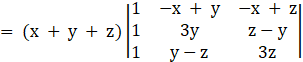[C1’ = C1/(x + y + z)]
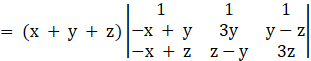[transforming row and column]
[C1’ = C1 - C2 & C2’ = C2 - C3]
= (x + y + z)[0 + 0 + ( - x - 2y)( - y - 2z) - ( - x + y)(2y + z)] [expansion by first row]
= (x + y + z)(xy + 2y2 + 2xz + 4yz + 2xy - 2y2 + xz - yz)
= (x + y + z)(3xy + 3yz + 3xz)
= 3(x + y + z)(xy + yz + zx)
1