Prove that = - (a – b) (b – c) (c – a) (a 2 + b 2 + c 2 ).

Question

Philoid · Accepted Answer

Operating R₁→R₁-R₂, R₂→R₂-R₃

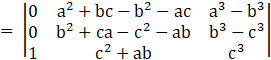
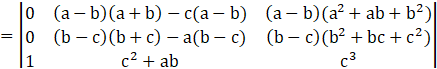
Taking (a-b), (b-c) common from R₁, R₂ respectively

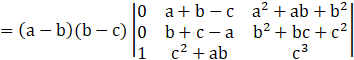
Operating R₁→R₁- R₂

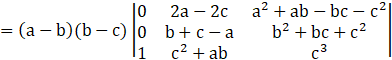
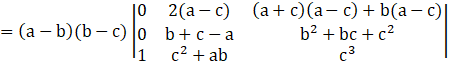
Taking (a-c) common from R₁

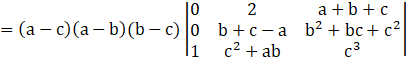
Expanding with C₁

= (a-c)(a-b)(b-c)×(2b²+2bc+2c²-ab-b²-bc-ac-bc-c²+a²+ab+ac)

=-(c-a)(b-c)(a-b)(a²+b²+c²)

Hence Proved

Prove that = - (a – b) (b – c) (c – a) (a2 + b2 + c2).