Let f : R → R be defined as 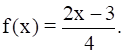Write fof –1 (1).

Question

Philoid · Accepted Answer

Formula:-

(i)A function f : X → Y is defined to be invertible, if there exists a function g : Y → X

such that gof =I_x and fog = I_y .The function g is called the inverse of f and is denoted by f^-1

(II)Let f : AB and g : BC be two functions.

Then, the composition of f and g, denoted by g o f, is defined as the function g o f : AC

given by g o f (x) = g (f (x))

Given:-

(i)f : R →R

F(y)=x

2y-3-4x=0

Now

Let f : R →R be defined as Write fof–1(1).