Let +6 (addition modulo 6) be a binary operation on S = {0, 1, 2, 3, 4, 5}. Write the value of 2 +6 4–1 +6 3–1.
From the definition of addition modulo :-
a*b =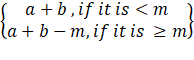 
(m is the base of the modulo)
Here the base is 6 and the set is S = {0,1,2,3,4,5}
So, we can make the composition table as :-
* | 0 | 1 | 2 | 3 | 4 | 5 |
0 | 0 | 1 | 2 | 3 | 4 | 5 |
1 | 1 | 2 | 3 | 4 | 5 | 0 |
2 | 2 | 3 | 4 | 5 | 0 | 1 |
3 | 3 | 4 | 5 | 0 | 1 | 2 |
4 | 4 | 5 | 0 | 1 | 2 | 3 |
5 | 5 | 0 | 1 | 2 | 3 | 4 |
It is clear that 1 is the identity element of this binary operation.
The inverse of 4 is 3 while the inverse of 3 is 4.
∴ 2 
4-1 
3-1 
= 2 
3 
4 = 3
1