Choose the correct answer

If then, =

We are given with

u = cot^-1{√tan θ} – tan^-1{√tan θ}

We need to find the value of .

Let √tan θ = x

Then, u = cot^-1{√tan θ} – tan^-1{√tan θ} can be written as

u = cot^-1 x – tan^-1 x …(i)

We know by the property of inverse trigonometry,

Or,

Substituting the value of cot^-1 x in equation (i), we get

u = (cot^-1 x) – tan^-1 x

Rearranging the equation,

Now, divide by 2 on both sides of the equation.

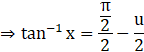
Taking tangent on both sides, we get

Using property of inverse trigonometry,

tan(tan^-1 x) = x

Recall the value of x. That is, x = √tan θ