Which of the following is not a convex set?

Given 4 sets,

i. {(x, y) : 2x + 5y < 7}

ii. {(x, y) : x² + y² ≤ 4}

iii. {x : |x| = 5}

iv. {(x, y) : 3x² + 2y² ≤ 6}

By graphing them, we can clearly figure out the convex set.

A convex set, is nothing but whose solution set is in the shape of a convex polygon.

i. {(x, y) : 2x + 5y < 7}

This inequation can be converted into an equation and by applying the intercept line format, we get,

[dividing the whole by 7]

We get,

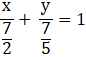
So the graph is

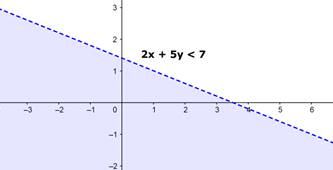
ii. {(x, y) : x² + y² ≤ 4}

So the graph for this inequality is given by

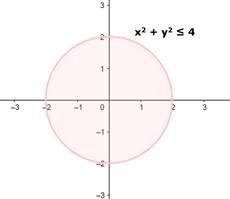
iii. {x : |x| = 5}

The graph for the set is as below:

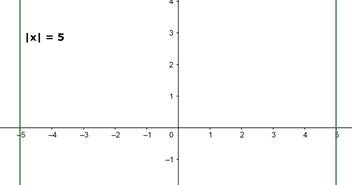
iv. {(x, y) : 3x² + 2y² ≤ 6}

The graph for the inequality is given by

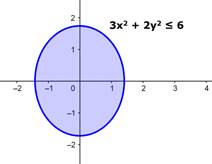
From t he above graphs, we can clearly say that, only the 3^rd graph is a convex set.

Hence option C is the answer.