Write the ratio in which the plane 4x + 5y – 3z = 8 divides the line segment joining points (–2, 1, 5) and (3, 3, 2).
We know that, the ratio in which the plane Ax + By + Cz + D=0 (where ![]() ) divides the line segment joining (x1, y1, z1) and (x2, y2, z2) then is given as,
) divides the line segment joining (x1, y1, z1) and (x2, y2, z2) then is given as,
![]()
Here, the equation of the given plane is, 4x + 5y–3z=8 i.e. 4x + 5y–3z - 8=0 and the co - ordinates of the two points are (–2, 1, 5) and (3, 3, 2).
Comparing with the general formula, we get,
A=4, B=5, C= - 3, D= - 8, x1= - 2, y1=1, z1=5and x2=3, y2=3 and z2=2.
So, the required ratio is
![]()
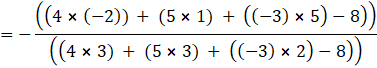
![]()
![]()
![]()
![]()
Hence, the plane 4x + 5y–3z=8 divides the line segment joining points (–2, 1, 5) and (3, 3, 2) in 2:1 ratio.
1