Find the vector equation of a plane which is at a distance of 5 units from the origin and its normal vector is .

From the given vector normal to the required plane, we can write the equation of the plane as,

[where, d is a constant]

…………………… (1)

We know, that the distance of a point (x₀, y₀, z₀) from a plane Ax + By + Cz + D=0 …………… (2) is

On comparing, equation (1) i.e. 2x - 3y + 6z + D=0 with

equation (2) we get,

A=2, B= - 3, C=6, D= - d.

Again, we know that, the co - ordinates of the origin are

(0, 0, 0).

So, the length of the perpendicular drawn from the origin is

Here, it is given that, the plane is at a distance of 5 units from the origin, so, we have,

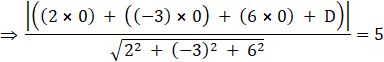
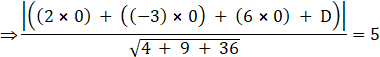
|D|=35

D=±35

∴d=± 35 [∵ D= - d]

Hence, the vector equation of a plane which is at a distance of 5 units from the origin and whose normal vector is is, 2x - 3y + 6z - ( - 35)=0 i.e. 2x - 3y + 6z + 35=0 or 2x - 3y + 6z - 35=0.

Hence, required equation of the plane, is i.e. 2x - 3y + 6z + 35=0 or, i.e. 2x - 3y + 6z - 35=0.