Mark the correct alternative in the following:
The distance of the line 
from the plane 
is
We have the, straight line given as,
and the plane as,
i.e. x - 5y + z=5 x - 5y + z - 5=0
Let us, check whether the plane and the straight line are parallel using the scalar product between the governing vector of the straight line, 
, and the normal vector of the plane given as, 
. If the straight line and the plane are parallel the scalar product will be zero.
=1 - 5 + 4
=0
From the given equation of the line, it is clear that, (2, - 2, 3) is a point on the straight line.
Distance from point (2, - 2, 3) to the plane, will be equal to the distance of the line from the plane.
We know, that the distance of a point (x0, y0, z0) from a plane Ax + By + Cz + D=0 …………… (2) is
On comparing, equation (1) i.e. x - 5y + z - 5=0 with
equation (2) we get,
A=1, B= - 5, C=1, D= - 5.
So, the distance from point (2, - 2, 3) to the plane
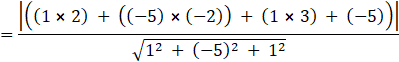
