Mark the correct alternative in the following:

The equation of the plane parallel to the lines x – 1 = 2y – 5 = 2z and 3x = 4y – 11 = 3z – 4 and passing through the point (2, 3, 3) is

The required plane is parallel to the lines

x–1=2y–5=2z and 3x=4y–11=3z–4.

Equation of the lines can be re - written as,

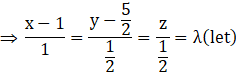
And,

So, we have the straight lines as,

And,

We have the normal vector of the plane as,

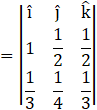
So, the equation of plane is , where

[∵the plane passes through the point (2, 3, 3)]

x - 4y + 2z= - 4

x - 4y + 2z + 4=0

The equation of the plane parallel to the lines

x–1=2y–5=2z and 3x=4y–11=3z–4 and passing through the point (2, 3, 3) is x–4y + 2z + 4=0