Write the value of the determinant .

Let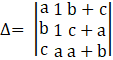

Using the property that if the equimultiples of corresponding elements of other rows (or columns) are added to every element of any row (or column) of a determinant, then the value of determinant remains the same.

Using column transformation, C₁→C₁+C₃

We get,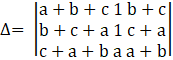

Using the property that if each element of a row (or a column) of a determinant is multiplied by a constant k, then its value gets multiplied by k.

Taking out factor(a+b+c) from C₁,

We get,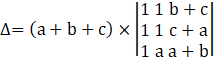

Using column transformation, C₁→C₁-C₂

We get,

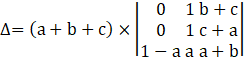
Expanding along C₁, we get

∆ =(a + b + c)×[(1-a)(c + a-(b + c))]=(1-a)(a-b)(a + b + c)