A matrix of order 3 × 3 has determinant 2. What is the value of |A(3I)|, where I is the identity matrix of order 3 × 3.

We are given that,

Order of a matrix = 3 × 3

Determinant = 2

I = Identity matrix of order 3 × 3

We need to find the value of |A(3I)|.

Let the given matrix be A.

Then, |A| = 2

Also, since I is an identity matrix, then

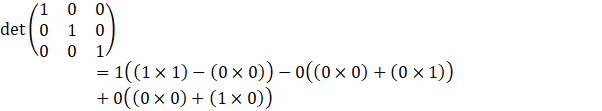
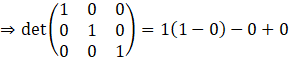
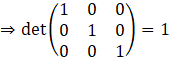
⇒ Det (I) = 1

Or,

|I| = 1

Then, we can say

3(I) = 3

⇒ 3I = 3

Thus,

|A(3I)| = |A(3)| [∵, 3I = 3]

⇒ |A(3I)| = |3A|

By property of determinants, we know that

|KA| = Kⁿ|A|, if A is of n^th order.

⇒ |A(3I)| = 3³|A| [∵, A has an order of 3 × 3 ⇒ |3A| = 3³ |A|]

⇒ |A(3I)| = 27 |A|

Since, |A| = 2. Then,

⇒ |A(3I)| = 27 × 2

⇒ |A(3I)| = 54

Thus, |A(3I)| = 54.