If . Write the cofactor of the element a₃₂.

We are given that,

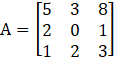
We need to find the cofactor of the element a₃₂.

A cofactor is the number you get when you remove the column and row of a designated element in a matrix, which is just a numerical grid in the form of a rectangle or a square. The cofactor is always preceded by a positive (+) or negative (-) sign, depending whether the element is in a + or - position. It is

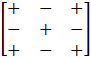
Let us recall how to find the cofactor of any element:

If we are given with,

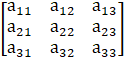
Cofactor of any element, say a₁₁ is found by eliminating first row and first column.

⇒ Cofactor of a₁₁ = a₂₂ × a₃₃ – a₂₃ × a₃₂

The sign of cofactor of a₁₁ is (+).

And, cofactor of any element, say a₁₂ is found by eliminating first row and second column.

⇒ Cofactor of a₁₂ = a₂₁ × a₃₃ – a₂₃ × a₃₁

The sign of cofactor of a₁₂ is (-).

So,

In matrix, .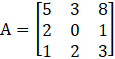

Element at a₃₂ = 2

We need to find the cofactor of 2 at a₃₂.

And as discussed above, the sign at a₃₂ is (-).

For cofactor of a₃₂, eliminate third row and second column in the matrix.

⇒ Cofactor of a₃₂ = 5 × 1 – 8 × 2

⇒ Cofactor of a₃₂ = 5 – 16

⇒ Cofactor of a₃₂ = -11

Since, the sign of cofactor of a₃₂ is (-), then

Cofactor of a₃₂ = -(-11)

⇒ Cofactor of a₃₂ = 11

Thus, cofactor of a₃₂ is 11.