If , then for any natural number, find the value of Det(Aⁿ).

We are given that,

We need to find the det(Aⁿ).

To find det(Aⁿ),

First we need to find Aⁿ, and then take determinant of Aⁿ.

Let us find A².

A² = A.A

Let,

For z₁₁: Dot multiply the first row of the first matrix and first column of the second matrix, then sum up.

That is,

(cos θ, sin θ).(cos θ, -sin θ) = cos θ × cos θ + sin θ × (-sin θ)

⇒ (cos θ, sin θ).(cos θ, -sin θ) = cos² θ – sin² θ

By algebraic identity,

cos 2θ = cos² θ – sin² θ

⇒ (cos θ, sin θ).(cos θ, -sin θ) = cos 2θ

For z₁₂: Dot multiply the first row of the first matrix and second column of the second matrix, then sum up.

That is,

(cos θ, sin θ)(sin θ, cos θ) = cos θ × sin θ + sin θ × cos θ

⇒ (cos θ, sin θ)(sin θ, cos θ) = sin θ cos θ + sin θ cos θ

⇒ (cos θ, sin θ)(sin θ, cos θ) = 2 sin θ cos θ

By algebraic identity,

sin 2θ = 2 sin θ cos θ

⇒ (cos θ, sin θ)(sin θ, cos θ) = sin 2θ

Similarly,

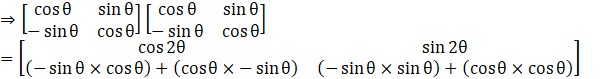
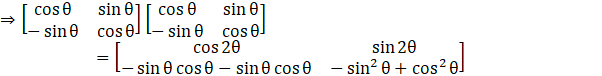
If and , then

Now, taking determinant of Aⁿ,

Determinant of 2 × 2 matrix is found as,

So,

Det(Aⁿ) = cos nθ × cos nθ – sin nθ × (-sin nθ)

⇒ Det(Aⁿ) = cos² nθ + sin² nθ

Using the algebraic identity,

sin² A + cos² A = 1

⇒ Det(Aⁿ) = 1

Thus, Det(Aⁿ) is 1.